
Реально затягивает. Фриспины часто дают, слоты красивые. Иногда интерфейс подвисает, но терпимо. Решил скачать ЭпикСтар и не пожалел.
Эпикстар онлайн предлагает игрокам уникальное сочетание развлечений, технологий и безопасности. Платформа регулярно обновляет ассортимент слотов и настольных игр, обеспечивая доступ к свежим новинкам и классике азартного мира. Кроме того, предусмотрены масштабные бонусы от ЭпикСтар: от приветственных до сезонных, включая кэшбэк и персональные предложения для активных пользователей. Высокий уровень безопасности, лицензия Кюрасао и прозрачная система генерации случайных чисел создают доверие и позволяют сосредоточиться на развлечении.
Новичку важно понимать: Epicstar зеркало – это не просто “клон” сайта, а способ обходить блокировки и продолжать игру без потерь. Даже если основной ресурс недоступен, через зеркало можно делать ставки, участвовать в акциях и активировать бонусы.
Зеркала помогают сохранять прогресс и бонусы, что критично для тех, кто только начинает играть и еще не успел освоиться с платформой. Кроме того, это безопасный способ проверить все функции, не рискуя потерять средства. Где безопасно искать рабочие зеркала ЭпикСтар:
Сторонние ресурсы опасны – они могут быть мошенническими и привести к потере денег.
Если зеркала недоступны, для входа ЭпикСтар можно использовать:
Новичок всегда будет иметь подключение к платформе, сможет безопасно пополнять счет, активировать промо и участвовать во всех акциях.
Регистрация EpicStar – первый и самый важный шаг. Процесс максимально упрощен, так как надо заполнить несколько полей.
После активации можно войти в личный кабинет, пополнить счет, активировать промо и настроить уведомления. Платформа адаптирована для мобильных устройств, поэтому играть можно где угодно, сохраняя все функции полной версии.
Приложение EpicStar Casino создано для тех, кто предпочитает стабильность без ограничений браузера. Оно оптимизировано под Android и iOS, быстро устанавливается и обеспечивает полный доступ ко всем функциям казино. Основные преимущества приложения ЭпикСтар:
Установка приложения занимает меньше минуты. Для Android оно доступно на официальном сайте в формате APK-файла, а для iPhone – в App Store. Перед установкой система автоматически проверяет совместимость устройства и корректно подстраивает интерфейс под диагональ экрана.
Современные механики становятся ключевым трендом. Они делают игру динамичнее, позволяют влиять на исход раунда и добавляют больше стратегических решений. Среди них: Hold & Spin, Buy Bonus, Cluster Pays, Megaways, Multiplier Trail и Tumble.
| Механика | Описание | Примеры |
|---|---|---|
| Hold & Spin | Фиксация выигрышных символов с повторными вращениями для увеличения выигрыша | Money Train 4, Big Bass Bonanza, Fire in the Hole |
| Buy Bonus | Возможность сразу купить доступ к бонусному раунду без ожидания | Sweet Bonanza, Wanted Dead or a Wild, Gates of Olympus |
| Cluster Pays | Выигрыши начисляются за группы одинаковых символов, а не линии | Reactoonz, Jammin’ Jars, Sugar Rush |
| Megaways | Количество выигрышных комбинаций меняется с каждым спином | Bonanza, The Dog House Megaways, Extra Chilli |
Слот-раздел впечатляет не только количеством, но и разнообразием стилей. Здесь представлены мистические, приключенческие и классические слоты EpicStar с фруктами, а также тайтлы с прогрессивными джекпотами. Провайдеры, представленные в казино, включают Pragmatic Play, Relax Gaming, Nolimit City, BGaming и Push Gaming. Автоматы вроде Book of Shadows, Sugar Rush и Big Bass Amazon Xtreme демонстрируют разные подходы к бонусным раундам: от фриспинов с расширяющимися символами до накопительных множителей.

Помимо классических автоматов, казино ЭпикСтар предлагает интерактивные лайв-шоу и краш-игры, где решающую роль играют скорость реакции и чувство момента. Лайв-раздел представлен слотами вроде:
С живыми ведущими, эффектами реального казино и ставками в реальном времени.
Краш-слоты, такие как Aviator, Space XY и Coin Flip Crash, построены на принципе нарастающего коэффициента: чем дольше ждешь, тем выше выигрыш, но и риск потерять все возрастает. Этот жанр популярен у игроков, предпочитающих быстрые решения и высокий азарт.

Приветственный бонус является классическим элементом любой бонусной программы, и официальный сайт EpicStar не исключение. Его цель – сделать первые шаги игрока более комфортными и выгодными. Что предлагает казино:
Использовать приветственный бонус ЭпикСтар рекомендуется сразу после регистрации.

Одним из наиболее привлекательных инструментов является кэшбэк – возврат части проигранных средств. Это снижает общий риск и делает игру более комфортной. Основные параметры кэшбэка:
| Процент возврата | от проигрыша за неделю |
|---|---|
| Варианты активации | начисляется автоматически |
| Формат начисления | средства поступают на бонусный или основной баланс, в зависимости от типа кэшбэка. |
| Условия отыгрыша | минимальные требования к вейджеру, что делает его одним из самых удобных инструментов бонусной системы. |
Кэшбэк особенно полезен для гемблеров, предпочитающих стратегии с высокой волатильностью. Даже при серии неудач часть денег возвращается, что позволяет продолжать игровую сессию без дополнительных депозитов.
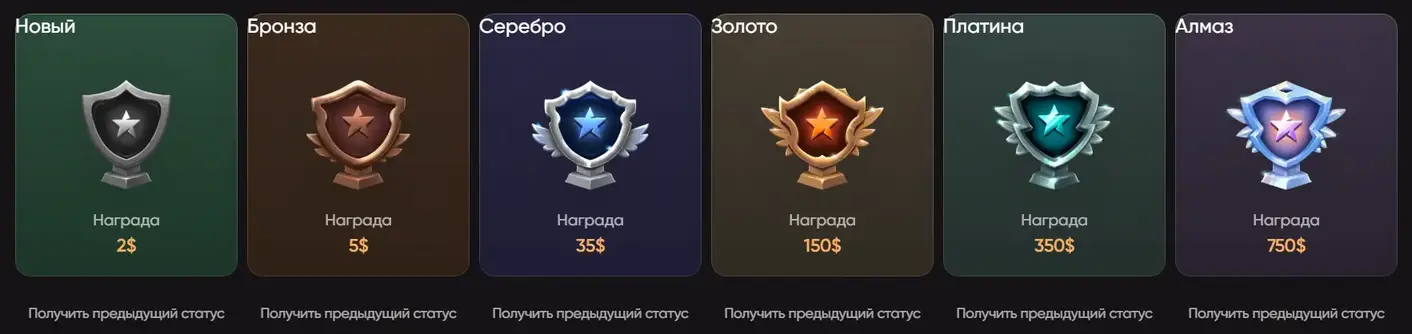
Доступна многоуровневая программа лояльности ЭпикСтар, которая вознаграждает постоянных игроков. Каждый уровень дает дополнительные привилегии, включая более высокие поощрения, ускоренные выплаты и эксклюзивные розыгрыши.
Очки лояльности начисляются за депозиты, ставки и участие в ивентах. Система стимулирует активность и делает привлечение постоянных игроков более выгодным как для бренда, так и для самих пользователей.
Регулярно проводятся сезонные события и раздает бонус-коды EpicStar, которые открывают доступ к уникальным бонусам. Варианты поощрений:
Использование промокодов ЭпикСтар – простой способ получить дополнительные преимущества. Обычно их активируют при пополнении баланса или через личный кабинет. Ивенты ограничены по времени, что стимулирует регулярное участие и внимательное отслеживание новых предложений.

Реально затягивает. Фриспины часто дают, слоты красивые. Иногда интерфейс подвисает, но терпимо. Решил скачать ЭпикСтар и не пожалел.

Нормальная площадка. Слоты интересные, лайв-рулетка супер. Деньги выводят быстро, бонусы бывают не часто, но приятные. Играть удобно, интерфейс понятный, а мобильная версия радует.

Заходит отлично! Интерфейс простой, слоты красочные, выигрыши иногда крупные. Мобильная версия реально удобная, можно играть где угодно.
1/1